History of Hexbin
In statistics, kernel density estimation (KDE) is a non-parametric way to estimate the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample. In some fields such as signal processing and econometrics, it is also termed the Parzen–Rosenblatt window method, after Emanuel Parzen and Murray Rosenblatt, who are usually credited with independently creating it in its current form. The software implementations of KDE led to the generation of various Density 2D charts, among which hexbin got popular for representing spatial data covering geographies.
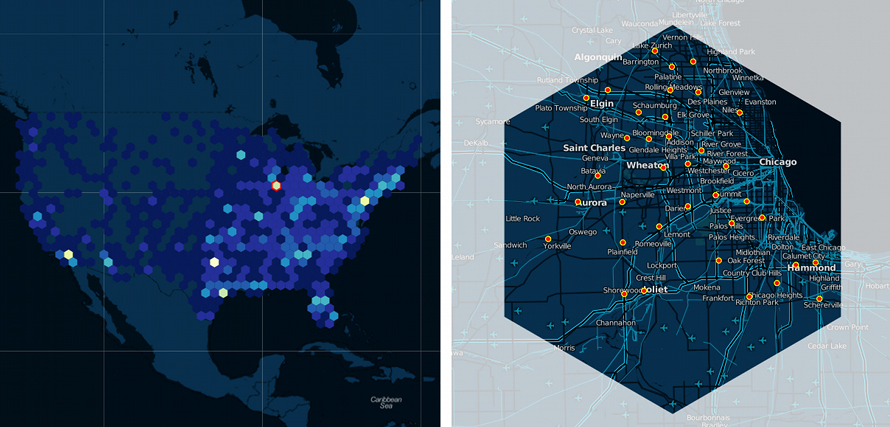
When to Use a Hexbin?
When you need to create an unbiased density distribution
Use Hexbin or grid map over choropleth maps as in choropleths, a large polygon’s data looks more emphasized just because of its size, introducing a bias in perception. With a hexbin, each region can be represented equally dismissing the bias. If your regions have a broad range of sizes and it introduces a bias for the audience it works better to consider using hexbin maps instead.
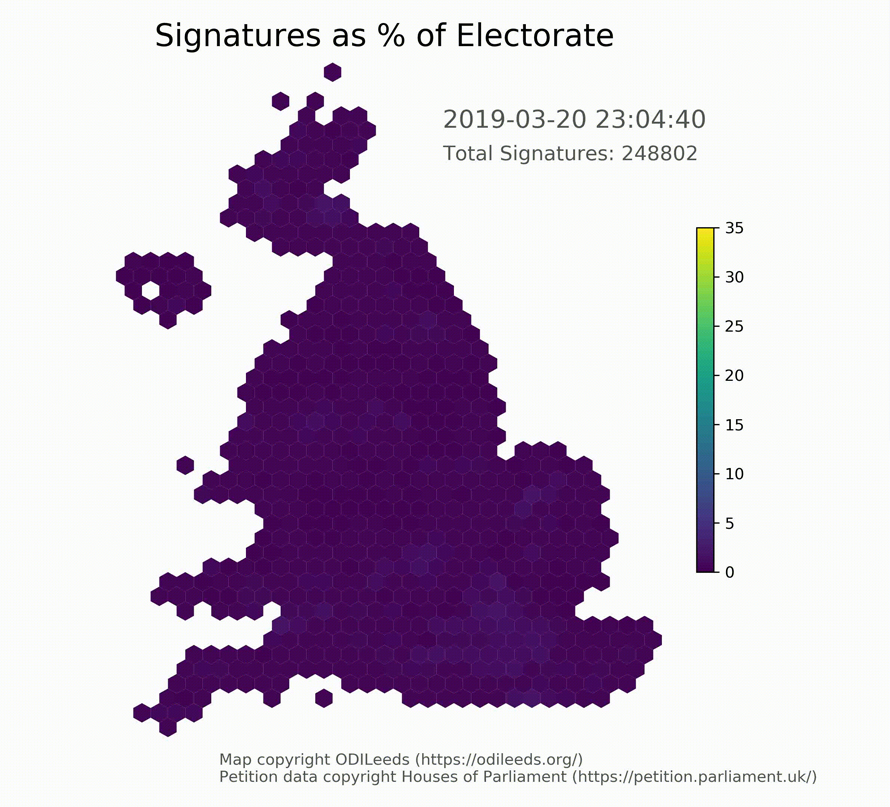
Understand part to whole relationships effectively
Use pie charts if your goal is to compare a given category (a slice of the pie) with the total (the whole pie) in a single chart and the multiple is close to 25 or 50 percent. In such a scenario a pie chart can often be more effective than a bar graph, working best with a few constituents. If the largest slices are placed from the top (like on a clock) and followed up with other slices, collectively, the data should add up to 100%.
When you need to explain and compare additional parameters through a circular representation
Use the different variants of pie charts like the Doughnut charts and the polar chart to represent additional information which cannot be represented in a standard Pie Chart. A polar chart, for instance, is a type of circular graph that can support multiple statistics at once and it provides a better data intensity ratio to standard pie charts. With doughnut charts, additional information can be represented in the center.
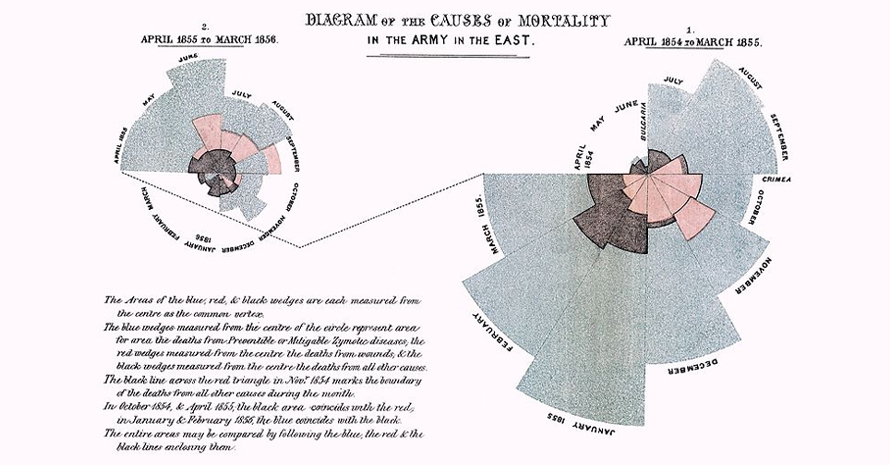
Polar chart by Florence Nightingale, 1858, If the death count in each month is subdivided by cause of death, it is possible to make multiple comparisons on one diagram
Types of Pie Charts
1. 3D pie chart /Perspective pie chart
This chart gives a 3D look and is often used for aesthetic reasons. However, the third dimension does not improve the reading of the data and is discouraged due to adding difficulty for interpretation.
2. Doughnut chart
This chart has a blank center allowing for additional information about the data as a whole to be included.
3. Exploded pie chart
Here one or more sectors separated from the rest of the disk. This effect is used to either highlight a sector or to highlight smaller segments of the chart with small proportions.
4. Polar area diagram
Here sectors have equal angles and differ rather in how far each sector extends from the center of the circle. The polar area diagram is used to plot cyclic phenomena (e.g., counts of births by month).
5. Ring chart, sunburst chart, and multilevel pie chart
This is used to visualize hierarchical data, depicted by concentric circles. A segment of the inner circle bears a hierarchical relationship to those segments of the outer circle which lie within the angular sweep of the parent segment.
6. Spie chart
This is a variant of the polar area chart which superimposes a normal pie chart with a modified polar area chart to permit the comparison of two sets of related data.
7. Square chart / Waffle chart
use squares instead of circles to represent percentages. Similar to basic circular pie charts, square pie charts take each percentage out of a total of 100%.
When Not to Use a Pie Charts?
When there are many proportions to represent
Pie Charts become crowded and hard to read if there are too many pieces of data, even with data labels and numbers. This makes it difficult for readers to analyze and assimilate information quickly and make decisions.
When an accurate and an at a glance comparison is required
Do not use pie charts for efficient and quick visual comparison as you have to factor in angles and compare non-adjacent slices, creating complexity in comparing the data slices. To make decisions based on visual impact rather than data analysis leads readers to draw inaccurate conclusions. To allow quick comparison and measurement, bar graphs can represent data by length and are a better visualization.