History of Histogram
Karl Pearson introduced several now-commonplace statistical tools. One of these was the histogram, a diagram similar to a bar chart. The use of a histogram in statistics is to represent a set of continuous, rather than discrete, data. For this reason, Pearson explained that it could be employed as a tool in the study of history, for example, to chart historical time periods, and coined the name ‘histogram’ in 1891 to convey its use as a ‘historical diagram’.
When to Use a Histogram?
Compare the frequency of occurrence of quantitative data – Compare the height of bars
Use a histogram in data visualization when an entire range of values of continuous numerical data can be bucketed into a series of intervals—and then how many values fall into each interval can be counted. The bins (or intervals) must be adjacent and are often (but not required to be) of equal size. When these intervals are of equal width then the height of the bars is proportional to the frequency and can be used to compare the data.
Compare the frequency of occurrence of quantitative data – Compare bar area when intervals are unequal
In a histogram, it is the area of the bar that indicates the frequency of occurrences for each bin. This means that the height of the bar does not necessarily indicate the correct frequency, but the product of height multiplied by the width of the bin indicates the frequency of occurrences within that bin. When the bars are not equally spaced the height of the bin does not reflect the frequency and should not be used as criteria for comparison.
Get an overview of statistical anomalies in data
The use of a histogram in statistics is defined by the need to check the consistency of your process by understanding the spread of the data and discovering the outliers. They are also used to estimate where values are concentrated, what the extremes are, and identify any gaps or unusual values in your data distribution. Determine the mode of the distribution by finding the peak of the histogram, as the value which is most frequently occurring or has the largest probability of occurrence. For many phenomena, it is quite common for the distribution of the response values to cluster around a single mode (unimodal- normal distribution) and then distribute themselves with lesser frequency out into the tails. Similarly, discover for bi-modal or multi-modal datasets. This can help to diagnose problems such as the non-uniformity of data and study the cause of outliers.
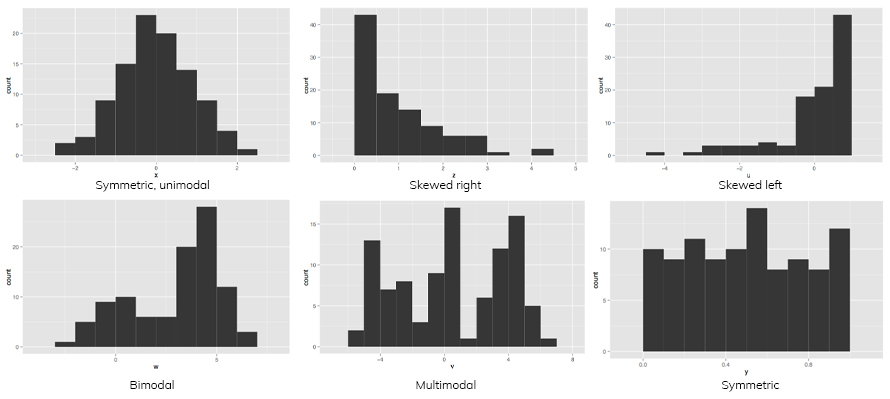
Represent and discover probability occurrences
Histograms are useful for giving a rough view of the probability distribution and are used to provide insight into their behavior and frequency of occurrence. For instance, In hydrology, the estimated density function of rainfall and river discharge data are analyzed using a probability distribution histogram graph.
Use histograms to give a rough sense of the density of the underlying distribution of the data for density estimation: when estimating the probability density function of the underlying variable. The total area of a histogram used for probability density is always normalized to 1. However, only nonnegative numbers can be used for the scale that gives us the height of a given bar of the histogram.
Types of Histograms
1. Equal bin width Histogram
If the bins are of equal size, a rectangle is erected over the bin with height proportional to the frequency—representing the equal bin width histogram.
2. Variable bin width histograms
When bins are not of equal width, the erected rectangle is defined to have its area proportional to the frequency of cases in the bin. The vertical axis is then not the frequency but frequency density—the frequency per unit of the class width on the horizontal axis.
3. Normalized or cumulative histograms
A histogram may also be normalized to display “relative” frequencies. It then shows the proportion of cases that fall into each of several categories, with the sum of the heights equaling 1.
When Not to Use a histogram?
When you need to show distribution against non-numerical categories
Do not use a histogram graph to plot the frequency of score occurrences in a non-continuous data set. Use bar charts for other types of variables including ordinal and nominal data sets since it’s a graph of categorical variables. The bar charts have gaps between the rectangles to clarify this distinction.
When you need to represent and discover correlations between two variables
Use a scatter plot when correlations between x and y-axis quantities are needed rather than to represent and gain an understanding of the distribution of a single variable across different intervals. Ask if you need to determine the way one variable changes with respect to the change in the other. In that case, you can use various correlation charts like line graphs, scatter plots, etc.