History of Venn Diagram
These charts were first mentioned in the 1880 paper entitled “On the Diagrammatic and Mechanical Representation of Propositions and Reasonings” in the Philosophical Magazine and Journal of Science. But the roots of these types of charts go back much further, at least 600 years. In the 1200s, philosopher and logician Ramon Llull of Majorca used a similar type of diagram. A German mathematician and philosopher Gottfried Wilhelm von Leibnitz is credited with drawing similar diagrams in the late 1600s. Venn diagrams are very similar to Euler diagrams, which were invented by Leonhard Euler in the 18th century.
When to Use a Venn Diagram?
To visualize the relationship between sets of items, such as commonalities and differences
Use Venn diagrams to visually organize information and compare products, services, processes, or anything that can depicted in sets. In data design, Venn diagrams are considered an effective communication tool to illustrate comparison. Through both elementary or advanced Venn diagrams, logical relationships could be visualized to represent intersections, unions, symmetric differences, and relative and absolute complements of sets.
To compare two or more choices and predict probabilities
Use Venn diagrams to predict the likelihood of certain occurrences. In statistics, several models are used for analysis of databases and Venn diagrams can, thus, be used to compare different sets of data and find degrees of commonality and differences. These correlations can help in the prediction of probabilities of certain occurrences. This aspect helps in the predictive analysis of datasets. Venn diagrams have been used also used to study the commonalities and differences among languages.
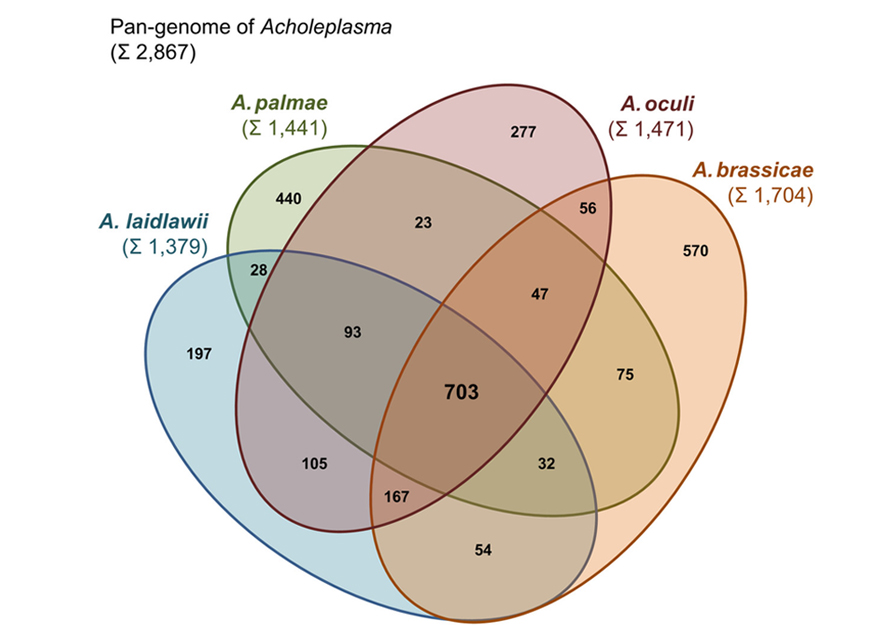
An area proportional Venn Diagram where each shape is proportional to the number of elements it contains
To reason through the logic
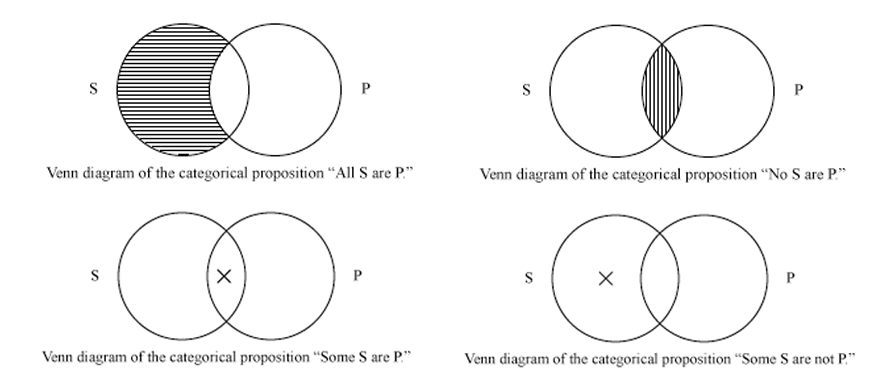
Venn diagrams are commonly used to determine the validity of particular arguments and conclusions. In deductive reasoning, if the premises are true and the argument form is correct, then the conclusion must be true. To reason through the logic behind statements or equations, such as the Boolean logic behind a word search involving “or” and “and”, statements can be visually represented through the diagrams.
In data design, Venn diagrams also correspond to truth tables for the propositions x in A, x in B, etc. in the sense that each region of the Venn diagram corresponds to one row of the truth table.
Types of Venn Diagram
1. Scaled Venn Diagram
This is also called as the area proportional diagram where the circles (or other shapes) are sized by their proportional representation of the whole.
2. Randolph diagram
R-diagram is a simple way to visualize logical expressions and combinations of sets, using intersecting lines.
3. Euler Diagram
This is a diagrammatic means of representing sets and their relationships, particularly useful for explaining complex hierarchies and overlapping definitions. However, unlike Venn diagrams, which show all possible relations between different sets, the Euler diagram shows only relevant relationships.
When Not to Use a Venn Diagram?
When there are many classes of objects to represent, Venn Diagrams become complex to understand
Do not use Venn diagrams when working on the analysis of databases leading to the reasoning focused on many classes of objects, as it becomes complicated to understand the information. Venn diagrams work well with at most three circles and going beyond that, making mistakes while encoding information can happen. It is possible to add more bounded regions if we are dealing with more than three classes, but then the resulting diagrams become rather difficult to handle and interpret.
When a clear comprehension is needed
Venn diagrams are limited in their nature. Even though we can seamlessly use them following data visualization design principles, they have limited expressive power in accurately representing pieces of information that cannot be accurately represented. For example, the system of notation allows us to talk about classes of objects, but not particular individual objects. We might have to introduce new symbols, using dots to represent individual objects.